Database Topics
References
- Advisor.com
- Database Management Student Resources
- LIS 558 - Database Management Systems and Programming
- What's The Greatest Software Ever Written?
IBM's System R, a research project at the company's Almaden Research Lab in San Jose, Calif., that gave rise to the relational database. In the 1970s, Edgar Codd looked at the math of set theory and conceived a way to apply it to data storage and retrieval. Sets are related elements that together make up an abstract whole. The set of colors blue, white, and red, for example, are related elements that together make up the colors of the French flag. A relational database, using set theory, can keep elements related without storing them in a separate and clearly labeled bin. It also can find all the elements of a set on an impromptu basis while knowing only one unique identifier about the set.
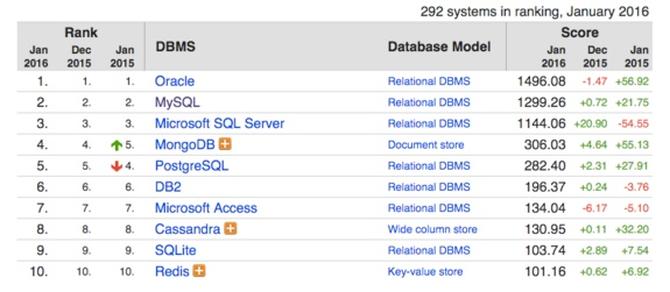
System R and all that flowed from it--DB2, Oracle, Microsoft SQL Server, Sybase, PostgreSQL, MySQL, and others--will have an impact that we're still just beginning to feel. Relational databases can both store data sets about customers and search other sets of data to find how particular customers shop. The data is entered into the database as it's acquired; the database finds relationships hidden in the data. The relational database and its SQL access language let us do something the human mind has found almost impossible: locate a broad set of related data without remembering much about its content, where it's stored, or how it's related. All that's needed is one piece of information, a primary key that allows access to the set. I like System R for its incredible smoothness of operation, its scalability, and its overwhelming usefulness to those who deal with masses of data. It's software with a rare air of mathematical truth about it.
- CourseWare | Training Software | Tutorials | Online instruction
Cardinality
- Minimum cardinality for relations (tables) A and B
- oval = optional
- hash line = mandatory = required
- Ask the questions:
- If there is an instance of A, must there also be an instance of B?
- If there is an instance of B, must there also be an instance of A?
- Maximum cardinality
- Parent:Child relationship must be 1:M (One-to-Many)
- N = M = infinity symbol = Many
- N:M = Many-to-Many relationship = Intersection relations
- Create a third relation that represents the relationship itself.
- Decompose the N:M relationship into two 1:M relationships.
- The key for an intersection relation is always the combination of parent keys.
- The parent relations are both required (mandatory). A parent must exist for each key value in the intersection relation.
Entity Relationship Diagrams
Minimum cardinality
- The minimum number of values that an attribute may have within a semantic object.
- In a relationship between tables, the minimum number of rows to which a row of one table may relate in the other table.
- Must the entity instance be related to an entity instance in the other table?
- Must the entity exist in the relationship?
- A hash mark across the relationship line indicates that an entity must exist in the relationship and an oval across the relationship line indicates that there may or may not be an entity in the relationship.
The minimum number of instances of one entity that must participate in a relationship
- An instance of an entity can exist without being related to an instance of the other entity. Here the
minimum cardinality is 0.
- Minimum # of instances of entity B that may be associated with instance of entity A
- Optional cardinality
- minimum cardinality = 0 means optional participation
- Mandatory cardinality = Obligatory cardinality
- minimum cardinality = 1 means mandatory participation
Maximum cardinality
- Them maximum number of values that an attribute may have within a semantic object.
- In a relationship between tables, the maximum number of rows to which a row of one table may relate in the other table.
- The maximum number of entities that can be involved in a relationship.
Anomalies = modification anomalies = deletion anomalies and/or insertion anomalies
- Insertion anomaly
- When the storing one row in a table records two separate facts.
- Facts about two or more different themes must be added to a single row of a relation.
- To add a complete a row to a table, one must add facts about two or more logically different themes.
- Deletion anomaly
- When the deletion of one row of a table eliminates two separate facts.
- Facts about two or more themes are lost when a single row is deleted.
- The removal of one row of a table deletes facts about two or more themes.
- Normalization
- Anomalies can be eliminated by redefining the relation into two or more relations. In most circumstances, the redefined, or normalized, relations are preferred.
- Referential integrity constraints avoid creating records in the "many" table for items that do not exist in the "one" table", etc...
-
Referential integrity = ensuring that the records in related tables are consistent with one another
- You can always delete a record from the "many" table.
- You can not delete a record from the "one" table when there are related records in the "many" table.
- Relaxing referential integrity: Cascaded deletion/updating of related/associated records.
-
Total Query (QBE Design view grid) performs calculations on a group of records using one of the summary (aggregate) functions. (Group by)
aggregate records / individual records.
-
Indexes should be specified for any criteria field in a query, as well as for any field that is used in a relationship to join two tables
- Anatomy of a Report
Report Header
Page Header
Group Header
Group Footer
Page Footer
Report Footer
- Report Types
- Columnar Report
- Tabular Report
- Summary Report
- Control Types
- Bound Control
- Unbound Control
- Calculated Control
 Databases Glossary
Databases Glossary